CPT Write Up
3a.
3.a.i.
This program is meant to provide users a way to efficiently use their time and improve their productivity.
3.a.ii.
In the video the user can input numbers and operation signs and the program would either output the answer to the expression or tell the user to try again with proper inputs. The program allows users to edit previous entries or delete them all.
3.a.iii.
The input of the program is a string of the desired equation to be solved. The user can input letters and signs. It also takes input from the user through the many buttons on the screen. The output as seen in the video is the answer to the expression.
3b.
3.b.i.

3.b.ii.
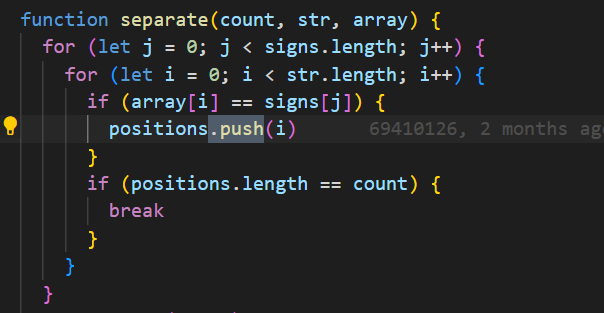
3.b.iii.
The name of the list being used is called positions.
3.b.iv.
The data contained in the list represents the positions of where the operator signs are in the expression that the user inputted. The positions are used to find out what the operators and the separate numbers the user wants to calculate with.
3.b.v.
The list manages complexity in my code because without it, I would have to write much more code of the program going through the user input, looking for the signs, then the numbers. This would mean the program would need to look for operators each time it wanted to find a new number, and do this until there are no longer any more operators, then the program would have to differentiate the operators from the numbers. Finally the program would be able to calculate the result.
3.c.
3.c.i.
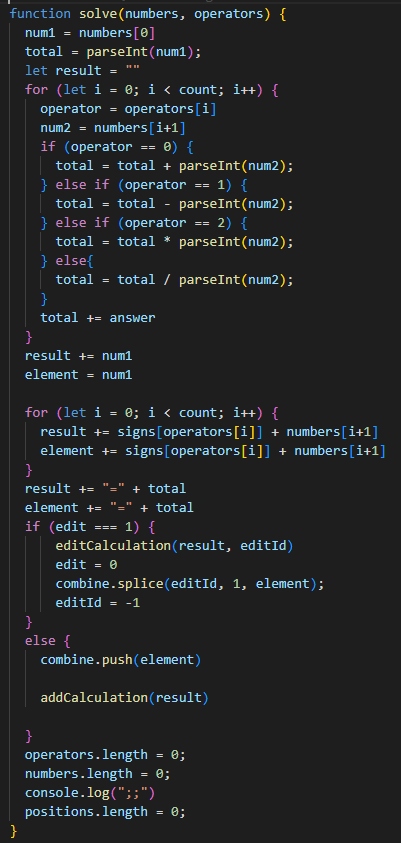
3.c.ii.
3.c.iii.
The procedure takes the numbers and operators from previous functions and uses it to calculate the expression. The function first begins with the first number, then uses the lists of each of the numbers and operators, and iterates through them and selects to determine whether to add, subtract, multiply, or divide. After determining the operator, it iterates to the next number and does the function, it iterates through the whole list and loops the process until it is finished. This allows the user to find the result of their problem.
3.c.iv.
First the function has two parameters of numbers and operators, which are lists of the numbers and operators.Then the program takes the first number and declares the total to be the first number. Then in a for loop, the program would loop the following process the same amount of times as the terms in the operators list. It would declare the operator in the loop to be the i’th term of the list and the number in the loop to be the i+1’th term since the first number was already in the total. There would be if and else if and else statements to determine which operation must take place. And in each statement would be the respective operation to add, subtract, multiply or divide the next number to the previous total. Once the total is found, there is another for loop that adds onto a string that would first add the first number, then iterate through the rest of the operators and numbers to prepare the expression and result to be outputted to the user.
3.d
3.d.i.
- Call One
- The first call would be: solve(numbers, operators) With numbers = [1,3] and operators = [0]
- Call Two
- The second call would be: solve(numbers, operators)
With numbers = [15,3] and operators = [3]
3.d.ii.
- The second call would be: solve(numbers, operators)
With numbers = [15,3] and operators = [3]
- Condition(s) tested by Call One
- The condition tested in Call One is to see the operator is equal to 0. It tests this to determine if it should add or not add, subtract or not subtract, multiply or not multiply, divide or not divide.
- Condition(s) tested by Call Two
- The condition tested in Call One is to see the operator is equal to 3. It tests this to determine if it should add or not add, subtract or not subtract, multiply or not multiply, divide or not divide.
3.d.iii.
- The condition tested in Call One is to see the operator is equal to 3. It tests this to determine if it should add or not add, subtract or not subtract, multiply or not multiply, divide or not divide.
- Results of Call One
- The result of call one would be 1+3 = 4. This shows that it is determined to add, not to subtract, not to multiply, and not to divide. So it added the two numbers together and outputted the plus sign.
- Results of Call Two
- The result of call one would be 15/3 = 5. This shows that it is determined not to add, not to subtract, not to multiply, but to divide. So it divided the two numbers and outputted the divide sign.