Hacks

3.9.1

  • why is it important to know that algorithms that look different can do the same thing and that algorithms that look the same might have different results?(0.15)
    • It is important to know that algorithms look different and that algorithms that look the same may have different results because when they look the same, a small difference can make it wrong. Also with different algorithms, it can do the same. It is important because I know that there are many ways to make an algorithm and I need to be careful when making algorithms.
  • for the converted conditional to boolean conversion(0.10)
isInedible = False
isLiquid = True

if isInedible == True:
    print("Don't drink it")
else:
    if isLiquid == True:
        print("Drink it")
    else:
        print("Don't drink it")

Drink it

isInedible = False
isLiquid = True

drinkTime = not(isInedible) and isLiquid
if drinkTime == False:
    print("Don't drink it")
if drinkTime == True:
    print("Drink it")

3.9.2

Develop your own complex algorithm using a flowchart and natural language, then code it!

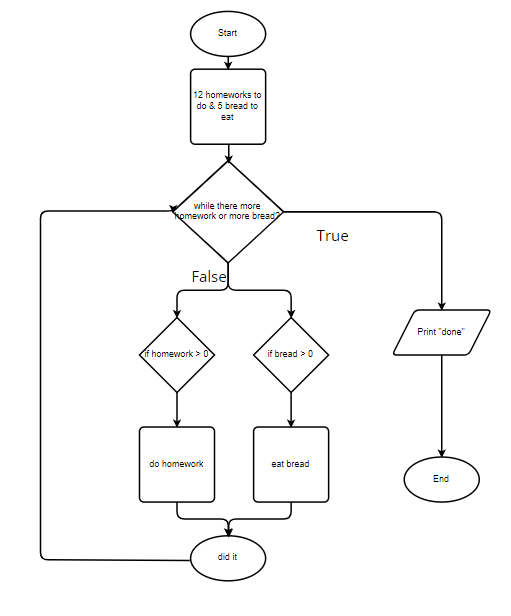
  1. Start
  2. There are 12 homeworks and 5 breads
  3. Repeat following steps 4-5 until there is no more bread or homework
  4. If there is more than one homework, do a homework
  5. If there is more than one bread, eat a bread
  6. Print done when finished
  7. Finish
homework = 12
bread = 5

while (homework or bread) > 0:
    if homework > 0:
        homework -= 1
    if bread > 0: 
        bread -= 1
print("Homework left:",homework,"\nBread left:",bread)

Homework left: 0 
Bread left: 0

3.9.3

Fix the number guessing game

  1. Make a flow chart for the algorithm number guessing game
  2. Make a function that gets the user guess
  3. Modify the existing search function to give more encouraging feedback

FLOWCHART:

import random

#sets variables for the game
num_guesses = 0
user_guess = -1
upper_bound = 100
lower_bound = 0

#generates a random number
number = random.randint(0,100)

# print(number)     #for testing purposes

print(f"I'm thinking of a number between 0 and 100.")

#Write a function that gets a guess from the user using input()
def guess():
    num = input("What number?")
    #add something here
    return num #add something here 

#Change the print statements to give feedback on whether the player guessed too high or too low
def search(number, guess):
    global lower_bound, upper_bound
    if int(guess) < int(number):
        print("Too low") #change this
        lower_bound = guess
        return lower_bound, upper_bound
    elif int(guess) > int(number):
        print("Too high") #change this
        upper_bound = guess
        return lower_bound, upper_bound
    else:
        upper_bound, lower_bound = guess, guess
        return lower_bound, upper_bound 

while user_guess != number:
    user_guess = guess()
    num_guesses += 1
    print(f"You guessed {user_guess}.")
    lower_bound, upper_bound = search(number, user_guess)
    if int(upper_bound) == int(number):
        break
    else:
        print(f"Guess a number between {lower_bound} and {upper_bound}.")

print(f"You guessed the number in {num_guesses} guesses!")

I'm thinking of a number between 0 and 100.
You guessed 50.
Too high
Guess a number between 0 and 50.
You guessed 25.
Too high
Guess a number between 0 and 25.
You guessed 15.
You guessed the number in 3 guesses!

3.11

  1. calculate the middle index and create a binary tree for each of these lists
    • 12, 14, 43, 57, 79, 80, 99
    • 92, 43, 74, 66, 30, 12, 1
    • 7, 13, 96, 111, 33, 84, 60
    • BELOW
  2. Using one of the sets of numbers from the question above, what would be the second number looked at in a binary search if the number is more than the middle number?
    • Set 1: 80, Set 2: 74, Set 3: 96

  3. Which of the following lists can NOT a binary search be used in order to find a targeted value?

    a. ["amy", "beverly", "christian", "devin"]

    b. [-1, 2, 6, 9, 19]

    c. [3, 2, 8, 12, 99]

    d. ["xylophone", "snowman", "snake", "doorbell", "author"]

    • C because it is unsorted
numListOne = [12,14,44,57,79,80,99]
numListTwo = [92,43,74,66,30,12,1]
numListThree = [7,13,96,111,33,84,60]
numLists = [numListOne, numListTwo, numListThree]
for x in range(len(numLists)):
    numLists[x].sort()
    middle = int(len(numLists[x])/2)
    print("Middle Index of List #",x+1,"is",numLists[x][middle])

Middle Index of List # 1 is 57
Middle Index of List # 2 is 43
Middle Index of List # 3 is 60