Data Structures- Space and Time Complexity
Observing the time complexity of different algorithms
- Space and Time Complexity
- Constant O(1)
- Linear O(n)
- Quadratic O(n^2)
- Logarithmic O(logn)
- Exponential O(2^n)
- Hacks
Space and Time Complexity
Space complexity refers to the amount of memory used by an algorithm to complete its execution, as a function of the size of the input. The space complexity of an algorithm can be affected by various factors such as the size of the input data, the data structures used in the algorithm, the number and size of temporary variables, and the recursion depth. Time complexity refers to the amount of time required by an algorithm to run as the input size grows. It is usually measured in terms of the "Big O" notation, which describes the upper bound of an algorithm's time complexity.
Why do you think a programmer should care about space and time complexity?
- A programmer should care about space and time complexity to ensure the program behaves properly in certain conditions and that it properly runs in a time period. The space complexity is the size of the input, which in turn makes the time complexity run more and more times to meet the larger input which makes the program take longer.
Take a look at our lassen volcano example from the data compression tech talk. The first code block is the original image. In the second code block, change the baseWidth to rescale the image.
from IPython.display import Image, display
from pathlib import Path
# prepares a series of images
def image_data(path=Path("ghtop_images/"), images=None): # path of static images is defaulted
for image in images:
# File to open
image['filename'] = path / image['file'] # file with path
return images
def image_display(images):
for image in images:
display(Image(filename=image['filename']))
if __name__ == "__main__":
lassen_volcano = image_data(images=[{'source': "Peter Carolin", 'label': "Lassen Volcano", 'file': "lassen-volcano.jpg"}])
image_display(lassen_volcano)
from IPython.display import HTML, display
from pathlib import Path
from PIL import Image as pilImage
from io import BytesIO
import base64
# prepares a series of images
def image_data(path=Path("ghtop_images/"), images=None): # path of static images is defaulted
for image in images:
# File to open
image['filename'] = path / image['file'] # file with path
return images
def scale_image(img):
#baseWidth = 625
#baseWidth = 1250
#baseWidth = 2500
baseWidth = 5000 # see the effect of doubling or halfing the baseWidth
#baseWidth = 10000
#baseWidth = 20000
#baseWidth = 40000
scalePercent = (baseWidth/float(img.size[0]))
scaleHeight = int((float(img.size[1])*float(scalePercent)))
scale = (baseWidth, scaleHeight)
return img.resize(scale)
def image_to_base64(img, format):
with BytesIO() as buffer:
img.save(buffer, format)
return base64.b64encode(buffer.getvalue()).decode()
def image_management(image): # path of static images is defaulted
# Image open return PIL image object
img = pilImage.open(image['filename'])
# Python Image Library operations
image['format'] = img.format
image['mode'] = img.mode
image['size'] = img.size
image['width'], image['height'] = img.size
image['pixels'] = image['width'] * image['height']
# Scale the Image
img = scale_image(img)
image['pil'] = img
image['scaled_size'] = img.size
image['scaled_width'], image['scaled_height'] = img.size
image['scaled_pixels'] = image['scaled_width'] * image['scaled_height']
# Scaled HTML
image['html'] = '<img src="data:image/png;base64,%s">' % image_to_base64(image['pil'], image['format'])
if __name__ == "__main__":
# Use numpy to concatenate two arrays
images = image_data(images = [{'source': "Peter Carolin", 'label': "Lassen Volcano", 'file': "lassen-volcano.jpg"}])
# Display meta data, scaled view, and grey scale for each image
for image in images:
image_management(image)
print("---- meta data -----")
print(image['label'])
print(image['source'])
print(image['format'])
print(image['mode'])
print("Original size: ", image['size'], " pixels: ", f"{image['pixels']:,}")
print("Scaled size: ", image['scaled_size'], " pixels: ", f"{image['scaled_pixels']:,}")
print("-- original image --")
display(HTML(image['html']))
Do you think this is a time complexity or space complexity or both problem?
- I think this is a problem of both time complexity and space complexity. The program repeats itself many more times when baseWidth gets longer. This is because the input of the image is a lot larger.
numbers = list(range(1000))
print(numbers)
print(numbers[263])
ncaa_bb_ranks = {1:"Alabama",2:"Houston", 3:"Purdue", 4:"Kansas"}
#look up a value in a dictionary given a key
print(ncaa_bb_ranks[1])
Space
This function takes two number inputs and returns their sum. The function does not create any additional data structures or variables that are dependent on the input size, so its space complexity is constant, or O(1). Regardless of how large the input numbers are, the function will always require the same amount of memory to execute.
def sum(a, b):
return a + b
print(sum(90,88))
print(sum(.9,.88))
Time
An example of a linear time algorithm is traversing a list or an array. When the size of the list or array increases, the time taken to traverse it also increases linearly with the size. Hence, the time complexity of this operation is O(n), where n is the size of the list or array being traversed.
for i in numbers:
print(i)
Space
This function takes a list of elements arr as input and returns a new list with the elements in reverse order. The function creates a new list reversed_arr of the same size as arr to store the reversed elements. The size of reversed_arr depends on the size of the input arr, so the space complexity of this function is O(n). As the input size increases, the amount of memory required to execute the function also increases linearly.
def reverse_list(arr):
n = len(arr)
reversed_arr = [None] * n #create a list of None based on the length or arr
for i in range(n):
reversed_arr[n-i-1] = arr[i] #stores the value at the index of arr to the value at the index of reversed_arr starting at the beginning for arr and end for reversed_arr
return reversed_arr
print(numbers)
print(reverse_list(numbers))
Time
An example of a quadratic time algorithm is nested loops. When there are two nested loops that both iterate over the same collection, the time taken to complete the algorithm grows quadratically with the size of the collection. Hence, the time complexity of this operation is O(n^2), where n is the size of the collection being iterated over.
for i in numbers:
for j in numbers:
print(i,j)
Space
This function takes two matrices matrix1 and matrix2 as input and returns their product as a new matrix. The function creates a new matrix result with dimensions m by n to store the product of the input matrices. The size of result depends on the size of the input matrices, so the space complexity of this function is O(n^2). As the size of the input matrices increases, the amount of memory required to execute the function also increases quadratically.
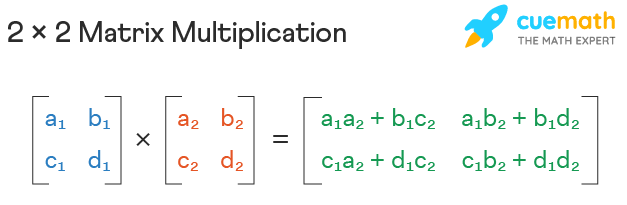
- Main take away is that a new matrix is created.
def multiply_matrices(matrix1, matrix2):
m = len(matrix1)
n = len(matrix2[0])
result = [[0] * n] * m #this creates the new matrix based on the size of matrix 1 and 2
for i in range(m):
for j in range(n):
for k in range(len(matrix2)):
result[i][j] += matrix1[i][k] * matrix2[k][j]
return result
print(multiply_matrices([[1,2],[3,4]], [[3,4],[1,2]]))
Time
An example of a log time algorithm is binary search. Binary search is an algorithm that searches for a specific element in a sorted list by repeatedly dividing the search interval in half. As a result, the time taken to complete the search grows logarithmically with the size of the list. Hence, the time complexity of this operation is O(log n), where n is the size of the list being searched.
def binary_search(arr, low, high, target):
while low <= high:
mid = (low + high) // 2 #integer division
if arr[mid] == target:
return mid
elif arr[mid] < target:
low = mid + 1
else:
high = mid - 1
target = 263
result = binary_search(numbers, 0, len(numbers) - 1, target)
print(result)
Space
The same algorithm above has a O(logn) space complexity. The function takes an array arr, its lower and upper bounds low and high, and a target value target. The function searches for target within the bounds of arr by recursively dividing the search space in half until the target is found or the search space is empty. The function does not create any new data structures that depend on the size of arr. Instead, the function uses the call stack to keep track of the recursive calls. Since the maximum depth of the recursive calls is O(logn), where n is the size of arr, the space complexity of this function is O(logn). As the size of arr increases, the amount of memory required to execute the function grows logarithmically.
Time
An example of an O(2^n) algorithm is the recursive implementation of the Fibonacci sequence. The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones, starting from 0 and 1. The recursive implementation of the Fibonacci sequence calculates each number by recursively calling itself with the two preceding numbers until it reaches the base case (i.e., the first or second number in the sequence). The algorithm takes O(2^n) time in the worst case because it has to calculate each number in the sequence by making two recursive calls.
def fibonacci(n):
if n <= 1:
return n
else:
return fibonacci(n-1) + fibonacci(n-2)
#print(fibonacci(5))
#print(fibonacci(10))
#print(fibonacci(20))
#print(fibonacci(30))
print(fibonacci(40))
Space
This function takes a set s as input and generates all possible subsets of s. The function does this by recursively generating the subsets of the set without the first element, and then adding the first element to each of those subsets to generate the subsets that include the first element. The function creates a new list for each recursive call that stores the subsets, and each element in the list is a new list that represents a subset. The number of subsets that can be generated from a set of size n is 2^n, so the space complexity of this function is O(2^n). As the size of the input set increases, the amount of memory required to execute the function grows exponentially.
def generate_subsets(s):
if not s:
return [[]]
subsets = generate_subsets(s[1:])
return [[s[0]] + subset for subset in subsets] + subsets
print(generate_subsets([1,2,3]))
print(generate_subsets([1,2,3,4,5,6]))
#print(generate_subsets(numbers))
Using the time library, we are able to see the difference in time it takes to calculate the fibonacci function above.
- Based on what is known about the other time complexities, hypothesize the resulting elapsed time if the function is replaced.
import time
start_time = time.time()
print(fibonacci(34))
end_time = time.time()
total_time = end_time - start_time
print("Time taken:", total_time, "seconds")
start_time = time.time()
print(fibonacci(40))
end_time = time.time()
total_time = end_time - start_time
print("Time taken:", total_time, "seconds")
Hacks
- Record your findings when testing the time elapsed of the different algorithms.
- When the loops in the program increase in linear length, the time complexity increases slightly. But when the loops and lengths increase exponentially, like counting 1000, 1000 times, the time complexity increases significantly more. If the program was way to big like the picture scaling one, the program Jupyter Kernel just crashed.
- Although we will go more in depth later, time complexity is a key concept that relates to the different sorting algorithms. Do some basic research on the different types of sorting algorithms and their time complexity.
- The best time complexity has the algorithm that takes the least amount of time and the worst time complexity, it iterates a bunch and too much that makes it really slow. Some types of sorting algorithms are Quick Sort and Bubble Sort. Quick Sort is one of the best sorting algorithm, it first picks a pivot point, them separates the values into two groups one bigger and one smaller than the pivot. Then it repeats this in each of the sub groups until the values are sorted. The Bubble Sort is pretty bad time complexity. It iterates through each element and sees if it and the next element are in the right order, if not it swaps it. It continues through the list. And it repeats the whole process until it is fully sorted. This takes really long with longer lists.
- Why is time and space complexity important when choosing an algorithm?
- Time complexity and space complexity are important when choosing an algorithm because if the input is small. The space complexity is going to be small. So if it is small the time complexity does not really affect the program's run length. But when the space complexity is really bad and large, the time complexity matters. So the algorithm needs to be the most efficient.
- Should you always use a constant time algorithm / Should you never use an exponential time algorithm? Explain?
- You should almost always you as constant time algorithm and should not use a exponential time algorithm. Constant time algorithms should be used because as the input sizes increase, the time algorithm does not increase by a lot but by a constant amount each increase. But with an exponential time algorithm, with larger input sizes the times would increase a bunch, kind of like an explosion.
- What are some general patterns that you noticed to determine each algorithm's time and space complexity?
- Some general patterns I noticed to determine each algorithm's time and space complexity were: For the fibonacci sequence my laptop could do the fibonacci(40) in 18 seconds without crashing. So my computer had enough memory and storage to do that. But for the counting to 1000, 1000 times, my computer took really long and it also crashed. So it had really bad time and space complexity. So for the time complexity, it would take really long. But for the bad space complexity, it would crash the kernel.
Complete the Time and Space Complexity analysis questions linked below. Practice
- I did the practice and for the first one I got the answer right. Because it is iterating until N and M, so it is O(N+M). For the second one, it iterated N, N times, so O(N*N). For number 3 I was confused on this. But apparently when doubling until n, that is log(n), but it is also doing it n times. So the answer is nlog(n). For the 4th question I got this right because I just knew it. For 5, it was dividing by 2 in a loop os it was O(log(n)). For 6 it was Time and Memory because that is space and time complexity. For 7, it was option 2 because that is what time complexity is. For question 8, it was confusing but from the explanation, it was looping k^n-1 times so the answer was O(logk(n)). For 9, it was n(n-1) because the inner loop runs n-1 times while the outer loop runs n times. For question 10 it is false because just because the worst case scenario says B always runs faster, A can still run faster in certain instances.